Algorithmic Robotics 

Algorithmic Robotics, at its core, delves into the intricacies of melding advanced algorithms with robotic systems to achieve optimal planning and control with efficiency. In the current literature landscape, this specialized field emphasizes concepts such as motion planning and optimal control strategies through the duality of probabilistic inference and optimization. Motion planning at the abstract level, such as policy blending, involves seamlessly integrating diverse decision-making rules to enhance a robot's adaptability in dynamic environments. Lower-level motion planning, such as trajectory optimization, on the other hand, focuses on refining the path and movement of robotic systems to achieve optimal performance, accounting for factors like energy efficiency and obstacle avoidance. Optimal control strategies further contribute by fine-tuning the robot's actions to maximize efficiency, often incorporating feedback mechanisms to adapt to changing conditions in real-time. These concepts become crucial building blocks in creating robots that execute tasks with precision and dynamically respond to the complexities of their surroundings, marking a significant leap forward in the synergy between algorithms and robotic capabilities. At IAS, we emphasize all aspects of Algorithmic Robotics, potentially off the mainstream deep learning research direction. Due to the chicken-and-egg problem of data in robotics, Algorithmic Robotics serves a vital role in robotics execution or data generation without any prior dataset.
Hierarchical Policy Blending for Reactive Motion Generation 
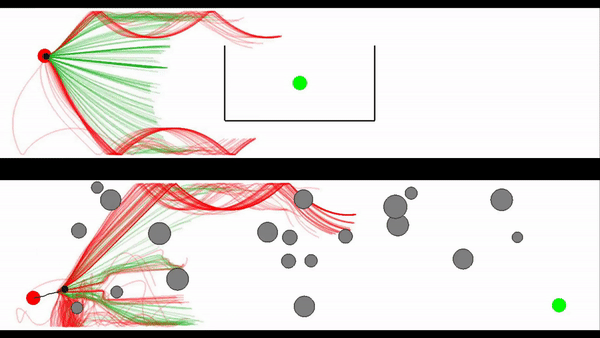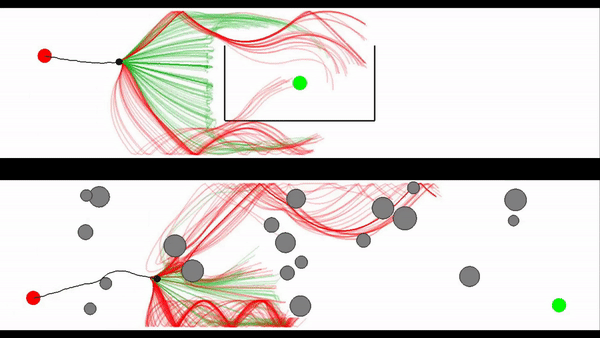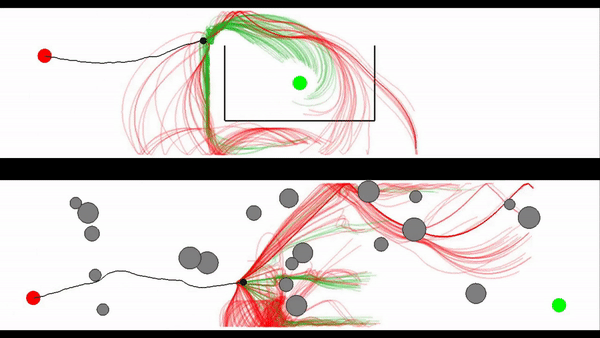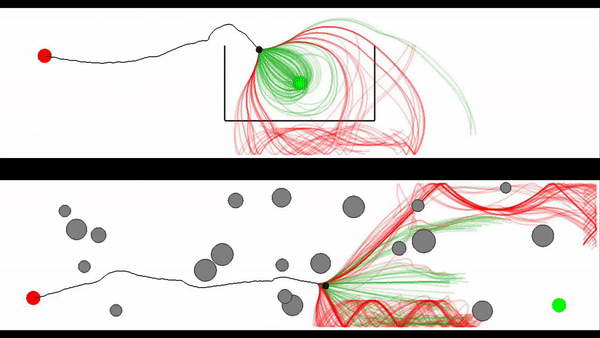
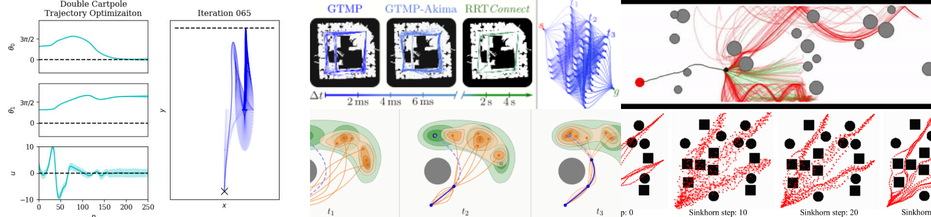
Motion generation in complex and dynamic environments is a central topic in robotics, rendered as a multi-objective decision-making problem. Balancing safety and performance, state-of-the-art methods trade-off between reactive policies and planning-based motion generation. To combine the benefits of reactive policies and planning, we introduced two novel hierarchical motion generation methods: Hierarchical Policy Blending as Inference (HiPBI) and Hierarchical Policy Blending as Optimal Transport (HiPBOT). Both techniques combine stochastic, reactive expert policies with planning, dynamically computing optimal weights over the task horizon. HiPBI employs probabilistic inference, framing policy blending as sampling-based stochastic optimization, while HiPBOT formulates it as deterministic entropic-regularized linear programming. Our methods effectively evade local optima, facilitating feasible reactive plans for navigating challenging dynamic environments.
- Hansel, K.; Urain, J.; Peters, J.; Chalvatzaki, G. (2023). Hierarchical Policy Blending as Inference for Reactive Robot Control, 2023 IEEE International Conference on Robotics and Automation (ICRA), IEEE.
- Le, A. T.; Hansel, K.; Peters, J.; Chalvatzaki, G. (2023). Hierarchical Policy Blending As Optimal Transport, 5th Annual Learning for Dynamics & Control Conference (L4DC), PMLR.
Batch Trajectory Optimization 

Motion planning is still an open problem for many disciplines, e.g., robotics, autonomous driving, due to their need for high computational resources that hinder real-time, efficient decision-making. A class of methods striving to provide smooth solutions is gradient-based trajectory optimization. However, those methods usually suffer from bad local minima, while for many settings, they may be inapplicable due to the absence of easy-to-access gradients of the optimization objectives. Via Optimal Transport theory, we propose how to scale gradient-free trajectory optimization to long-horizon, high-dimensional state-space and a number of plans. Batch planning methods are crucial for robotics since they could discover many homotopy classes in the multi-objective problems, thereby exhibiting robustness to bad local minima. Furthermore, these batch methods can serve as a strong oracle for collecting datasets or striving to discover a global optimal solution for robotics skill execution.
- Le, A. T.; Chalvatzaki, G.; Biess, A.; Peters, J. (2023). Accelerating Motion Planning via Optimal Transport, Advances in Neural Information Processing Systems (NIPS / NeurIPS).
- Le, A. T.; Chalvatzaki, G.; Biess, A.; Peters, J. (2023). Accelerating Motion Planning via Optimal Transport, IROS 2023 Workshop on Differentiable Probabilistic Robotics: Emerging Perspectives on Robot Learning, [Oral].
- Le, A. T.; Chalvatzaki, G.; Biess, A.; Peters, J. (2023). Accelerating Motion Planning via Optimal Transport, NeurIPS 2023 Workshop Optimal Transport and Machine Learning, [Oral].
Optimal Control 
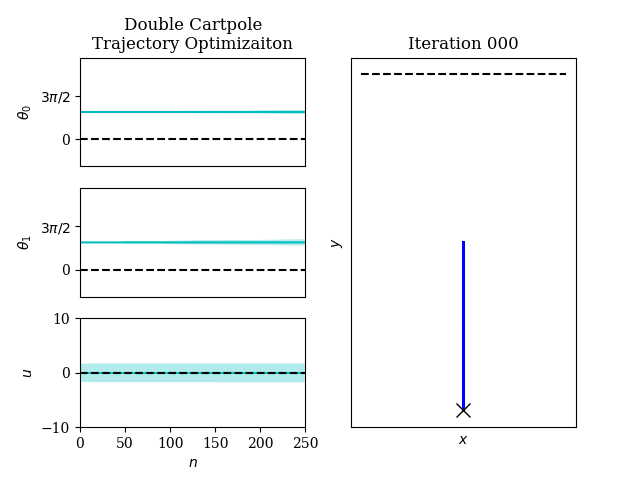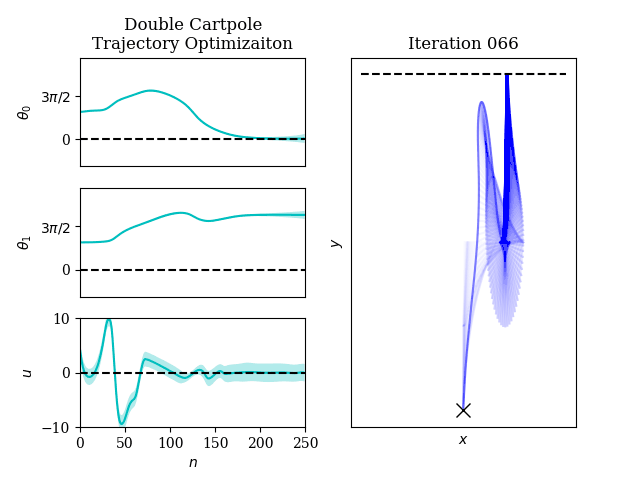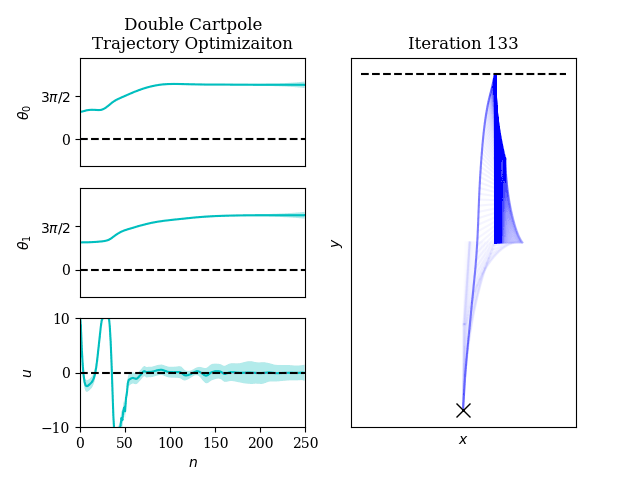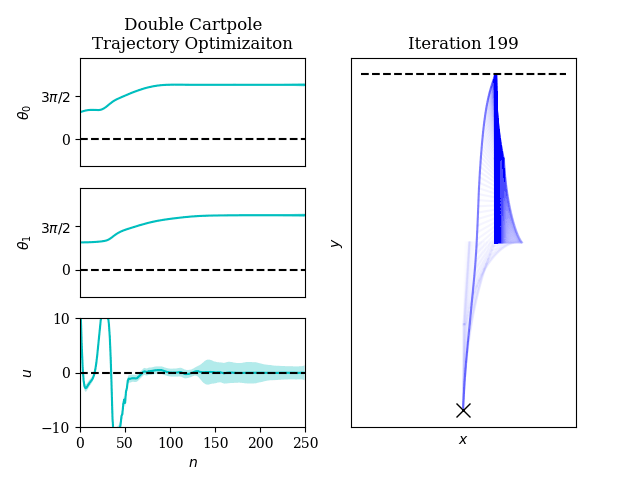
Optimal control is ubiquitous in robotics, from trajectory optimization to model predictive control.
Within the context of robot learning, we are interested in how statistical methods can be used to enhance stochastic optimal control algorithms and also how stochastic optimal control methods can be integrated with learning in reinforcement learning.
- Lioutikov, R.; Paraschos, A.; Peters, J.; Neumann, G. (2014). Generalizing Movements with Information Theoretic Stochastic Optimal Control, Journal of Aerospace Information Systems, 11, 9, pp.579-595.
- Belousov, B.; Neumann, G.; Rothkopf, C.; Peters, J. (2016). Catching Heuristics Are Optimal Control Policies, Advances in Neural Information Processing Systems (NIPS / NeurIPS).
- Akrour, R.; Abdolmaleki, A.; Abdulsamad, H.; Neumann, G. (2016). Model-Free Trajectory Optimization for Reinforcement Learning, Proceedings of the International Conference on Machine Learning (ICML).
- Arenz, O.; Abdulsamad, H.; Neumann, G. (2016). Optimal Control and Inverse Optimal Control by Distribution Matching, Proceedings of the International Conference on Intelligent Robots and Systems (IROS), IEEE.
- Watson, J.; Abdulsamad, H.; Peters, J. (2019). Stochastic Optimal Control as Approximate Input Inference, Conference on Robot Learning (CoRL).
- Watson, J.; Peters, J. (2022). Inferring Smooth Control: Monte Carlo Posterior Policy Iteration with Gaussian Processes, Conference on Robot Learning (CoRL).